
Съдържание
- Законът на Ципф обясни
- Основен експеримент
- Законът на Zipf в пазарите на Steam
- Какво можем да научим за Steam?
- Заключения
Преди малко един мой приятел предложи да гледам видео на Vsauces на закона на Цип, принципа на Парето и техните загадъчни изяви около нас. Ето малко закачка, за да привлечете вниманието ви - 80% от всички хора живеят в 20% от най-популярните градове; 80% от цялата земя принадлежи на 20% от най-богатите наемодатели; 80% от всички боклуци са на върха на 20% най-трохите улици - както се предвижда от закона на Цип и принципа на Парето.
Не достатъчно? Е, както открих вчера, заешката дупка не спира дотук ... Пълен със скептицизъм, реших да погледна колко време хората прекарват в играта на Steam ... Добре. 80% от времето на хората се изразходват за 20% от най-популярните игри ... Интересно? Е, прочетете, има още нещо в тази история.
Включването на повече от 20 минути, усилието на Vsauces е страхотно и обяснява много неща от голямата картина за Zipf, но той е много срамежлив да ни покаже основния механизъм, за който се смята, че допринася за това, защо Zipf работи. Така че, преди да продължим, бих искал накратко да обясня това.
Законът на Ципф обясни
Съществуват няколко концептуални начина да се обясни интуицията зад принципа 20/80. Най-добрият пример, според мен, е този за лунните кратери.
Основен експеримент
Така че, представете си, че ще останете недокоснати Луна - идеално гладка повърхност. Сега, да кажем, че има някои случайно оразмерени астероиди, които улучат Луната-неволю. Когато първите астероиди се приземят, той оставя кратер. Сега друг хитове, оставяйки кратер на друго място. Всеки кратер е част от общата площ, следователно има вероятност следващият случайен астероид да удари близо до съществуващ кратер и да се присъедини към него, образувайки група. Вероятността нов астероид да удари даден кратер е пропорционална на съществуващите размери на кратерите и астероидите. Това означава, че следващият случаен астероид е по-вероятно да се присъедини към най-голямата съществуваща група, което го прави още по-голям. Един вид кумулативен процес, който след това създава богати, по-богати, бедни механизми.
Имайте това предвид, защото се смята, че това е общото обяснение за "защо" законът на Zipfs работи с такава загадъчна универсалност. Астероидният пример е доста прост, но въпросът е какво ще се случи при много повторения
Малко объркващо?
Е, направих ги, за да задвижвам тази начална точка. NB! графиката ще бъде обсъдена по-късно, просто опитайте да си представите експеримента.

Ако наблюдаваме действителната Луна, се оказва, че тъй като количеството на астероидите се увеличава до големи количества, наблюдаваните диаметри на кратерите нарастват така, че 20% от най-големите кратери достигат 80% от цялата повърхност.
Тъй като отиваме към повече астероиди, разпространението на най-популярните и най-малко популярни групи подхожда към някакъв вид "идеално разпределение" с това свойство 20/80 - разпределението на Парето. Ако направите математика, се оказва, че (като цяло), ако най-голямата група има размер N, втората по големина група е около размер N / 2, третият N / 3 и така нататък и така нататък. Това се нарича Законът на Цип. Странното е, че законът на Ципф и разпределението на Парето работят за объркващо количество елементи (астероиди) и групи (клъстери на кратери). Разбира се, има изкривявания и случайни смущения, но общата тенденция е неоспорима.
Надявам се, че можете да видите как астероидите са по-склонни да удрят големи кратери на Луната и се свързват с по-привлекателните градове, ако вече има повече хора, които живеят в тях. Въпреки това, човек трябва да осъзнае, че градовете са далеч от единствените "групи", които се държат според Зипф.
Ето няколко примера от изследването на Марк Нюманс относно разпределенията на Парето. NB! Графиките са в log-log мащаб, който изглажда хиперболичната форма на кривите, представяйки почти линейна връзка.
Първоначално y = aX ^ (- b)
Дневник на двете страни => log y = log a - b log X
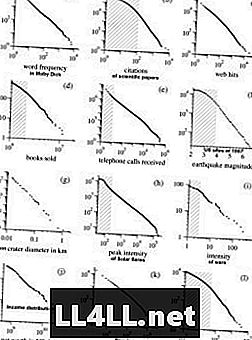
Интересното е, че същата тенденция се проявява и от религиозните култове ... Общата собственост на повечето от тези явления е просто тази тенденция „големи групи-да-по-големи“. Така законът на Ципф е постоянен в механизмите, където предпочитанията на елементите са положително свързани с размера на групите (което означава, че колкото по-голяма е групата, толкова по-вероятно е тя да расте). Ето защо обичам да мисля за групите като за клъстери и елементи като клъстери.
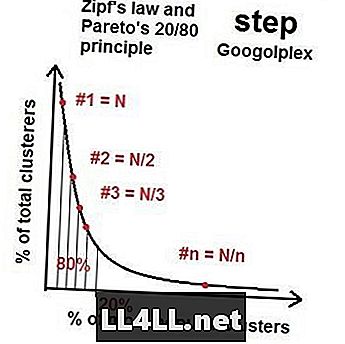
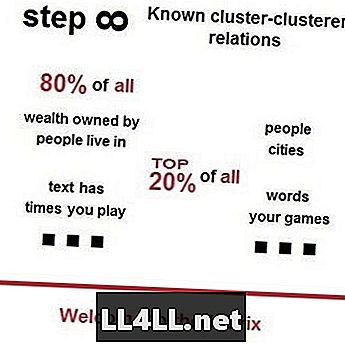
Законът на Zipf в пазарите на Steam
Подозрително за последното? Ето колко време хората харчат за най-популярните игри на Steam .. Данни от SteamSpy.
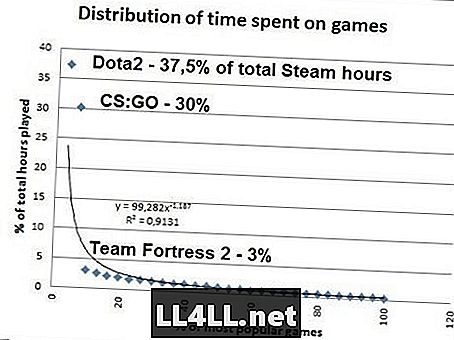
Ако се справите с математиката, се оказва, че 20% от най-популярните Steam игри заемат 80% от общата сума за игра, така че мистерията на Pareto 20/80 работи като чар тук ... Все пак трябва да се отбележи, че за Zipf да е истина, CS: GO трябва да отчита 37,5% / 2 = 18,8% от общото време, вместо огромни 30%. Но настрана от този отклонение (STOP PLAYING) CS: GO), Zipf-подобно разпределение е очевидно там.
Ето количеството продадени копия за най-популярните игри.
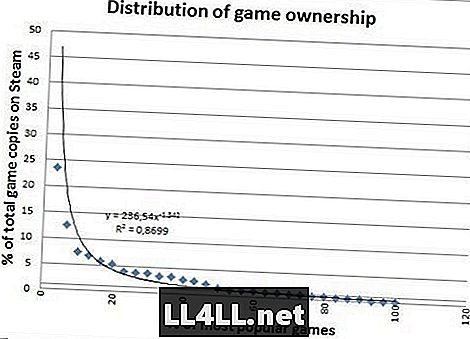
Изглежда много по-хубаво? Продадените копия нямат големи отклонения, така че се вписва много добре, което е забележителна разлика. Има обаче нещо по-интересно да се заключи от различията на последните две графики.
Забелязвате ли как „опашката“ вдясно е вид мазнина във втората графика? Казано по-просто, това ни казва, че "относително непопулярните" игри всъщност са доста по-популярни, отколкото в предишния заговор.
Всъщност се оказва, че 20% от най-популярните игри заемат едва 60% от продажбите, срещу 80% от играта. Интересно? Обзалагате се, че това е така.
Какво можем да научим за Steam?
Фактът, че популярността на игрите следва разпределението на Парето ни казва, че наистина има някакъв положителен мрежов ефект, който кара играчите да избират игри, които вече се играят от повече хора. Каква е разликата в пълнотата на опашките ни казва, че потребителите на Steam са много по-слепи от групата, когато купуват игри, отколкото са, когато ги играят.
Помислете за това - колкото повече хора купуват игри, независимо от „текущото обществено мнение“, толкова по-изгладени са дистрибуциите на Парето, тъй като е по-малко вероятно големите игри да продължат да растат. Ако никой не е давал на плъхове колкото повече хора играят игра, а наличността на всички игри е същата, тогава бихме очаквали 20% от най-популярните игри да заемат около 50% от продажбите и времето за игра (например приемането на индивидуални предпочитания са нормално разпределени).
Заключения
Така че има два фактора, които допринасят за разпространението на Парето в пазарите на Steam - колко иновативни са разработчиците (колко нови лъжливи луни се формират) и колко геймърите (астероидите) оценяват размера на текущата група, когато избират коя група да се присъединят , Както се оказва, геймърите са много близки по размер на групата, когато купуват игри, но точно обратното, когато ги играят. Готино, нали?
Ако искате да научите повече за дистрибуциите на Law и Power Law, тук е хубава лекция. Освен това, не забравяйте да погледнете хартията на Нюман!
Ако искате да прочетете повече от този вид неща, достатъчно скоро ще се опитам да се присъединя към това наблюдение към модел, който показва, че по-популярните мултиплейър игри имат по-високи цени (които са свързани с предпочитанията на играчите да се присъединят към групи с по-голям размер). Вижте статията тук. Статията на Piece De Resistance ще се опита да се присъедини към тези теории, като обясни как многобройните игри, социалните мрежи и градовете са всъщност всички анти-конкурентни стоки с мрежови ефекти (колкото повече хора консумират стока, толкова повече ползи за всеки отделен потребител), което има озаглавил ги с тази мъгла на ципфианската мистерия ...
Дотогава - насладете се!
Послепис Попълнете коментар със забавна идея за отношение 20/80, което според вас може да е вярно.
Моите са:
80% от носталгията на хората е причинена от 20% от техните най-щастливи спомени (действително доказани за степента, в която хората забравят информацията)
80% от масата е концентрирана в 20% от най-големите космически обекти (действително доказани за разпределение на гравитационната сила)
И разбира се
80% от бъркотията във вашата тоалетна идва от 20% от това, което ядете (без академични изследвания)